石英晶体振荡器,石英晶体的原子面系数

石英晶体的原子面符号

石英晶体和非晶体本质差别在于它们的内部结构是否存在周期性。为了描述晶体结构的周期性,用空间点阵来模拟晶体内部结构。通过点阵的“点子”作三组向不同的平行线,就构成了空间格子,称为“晶格”,如图1.2.1。

图1.2.1晶格示意图

整个空间格子是由一个单元重复排列的结果,这个重复单元就称为“晶胞”。晶胞是石英晶体结构的基本单元,晶胞的形状和大小由晶胞参数(晶胞的几个边长和这几个边长之间的夹角)来决定。晶胞的选择不是唯一的,除反映晶体内部的周期性外,还要反映晶体的外部对称性。

石英晶体的晶胞是选择如图1.2.2所示的六角晶胞,其晶胞参数为c=b=d4.9404A;c=5.394A;a=B=90°y=120°

图1.2.2六角晶胞示意图

在晶体点阵中,通过任一点子,可以作全同的原子面和一原子面平行,构成一族平行原子面。这样一族原子面包含了所有点子,它们不仅平行而且等距,各原子面上点子分布情况相同。晶体中有无限多族平行原子面。不同族原子面在石英晶振晶体中的方位不同,原子面的间距不同,原子在原子面上的分布不同,相应的物理性质也不同。因此,我们用原子面指数来表示该族原子面的方位,代表该族原子面。为了表明各个原子面,一般采用原子面指数(hk)表示,只有三角晶系和六角晶系才采用原子面指数(hki1)表示,现分别介绍如下。

一、一般晶系原子面指数表示法

从几何学中知道要描述一个平面的方位,就要选一个坐标系,然后标出这个平面在此坐标轴上的截距,或标出这个平面的法线在此坐标系中的方向余弦,描述原子面的方位也是如此。选某一原子(或离子、分子)的重心为坐标原点,以晶胞的三个边a、b、c(即晶轴)为坐标系,但应注意：

(1)由贴片晶振晶轴组成的坐标系不一定是直角坐标系

(2)晶轴上的长度单位分别为晶格常数a、b、c,所以截距的数值是相应晶格常数的倍数。

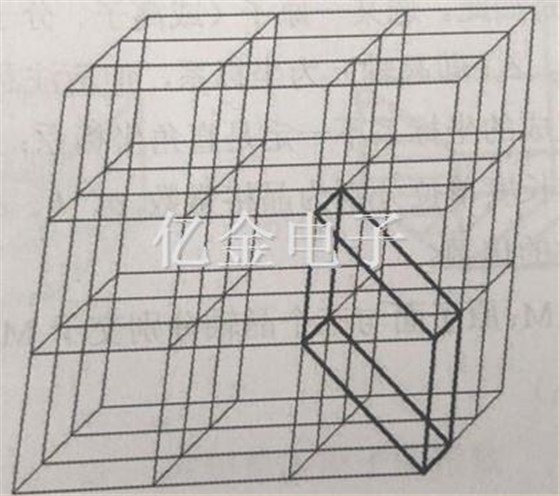
例如M1、M2、M3原子面与三个晶轴分别交于M1、M2、M3点,如图1.2.3所示,三个截距为

图1.2.3(236)原子面

知道了原子面在坐标中的截距,就等于知道原子面在晶体中的方位,所以也可用截距p、q、r来标志原子面,但由于原子面与某晶轴平行时相应的截距为无限大,为了避免出现无限大,改用截距倒数的互质比。

来标记原子面,为了简化常略去比例记号,采用(hk)表示,(hk)就称为原子面指数(或晶面指数、密勒指数),例如图1.2.3中原子面指数为(2,3,6)即：

原子面指数

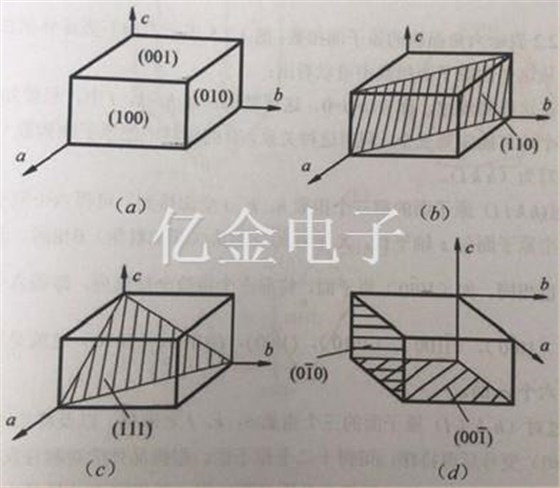
有时也称MM2M3平面为(2,3,6)原子面,图1.2.4中标出了一些简单的原子面指数,因为有源晶振,石英晶振晶轴有正向、负向之分,所以原子面指数也有正、负之分,通常将负号写在指数的上面,例如(010)原子面,就表示原子面与a轴、c轴平行,与b轴的截距为-b。

图1.24一些简单的原子面指数

六角晶系和三角晶系原子面指数表示法上述原子面表示法可用于全部晶系,具有普遍性,但在六角晶系中采用四个晶轴的坐标系比较方便,四个晶轴中的a、b、d、轴在同一平面上,互成120°0,夹角,c轴则与此平面垂直。原子面指数(hk1)中h、k、i、l则分别对应于a、b、d、c轴截距倒数的互质比。例如,某原子面与四个晶轴分别交于M1M2M3M4点,如图1.2.5所示四个截距为

OM2=pa=4a

OM2=qb=4b

OM3=rc=2c

OM4=td=-2d

1.2.5原子面

图1.2.5(1122)原子面

这些截距倒数的互质比为

截钜互质比可见图M1M2M3M4面的原子面指数为(1122)。

图12.2表示六角晶胞的原子面指数,图1.2.5表示右旋石英晶振,石英晶体的部分原子面指数,从这些的原子面指数中可以看出:

(1)存在这样的规律,即h+k+i=0。这就是说,在h,k,i中,只要知道其中两个即可确定第三个,利用这种关系,有的资料中把原子面指数(h k i l)简写为(h k l)。

(2)通过(hkiD)原子面的前三个指数h,k,i全部排列,可得六个原子面,这六个原子面与z轴平行,X射线的反射角(即掠射角) θ相同。其物理性质也相同。如(1010)原子面,将前三个指数全部排列,即得六个原子面为(1010),(1100),(0110),(100),(0110),(1010)这就是石英晶体的六个m面。

(3)通过对(hki1)原子面的三个指数h,k,l全排列,以及将第四个指数l(l0)变号后再排序,可得十二个原子面,根据晶体的对称性发现这十个原子面可分为二组,每组六个原子面,同一组原子面的性质完全相同例如:(1011)原子面,将前三个的指数全排列,即得六个原子面为(101i),(1101),(0111),(1101),(011),(1011)将第四个指数变号后,再全排列,又得六个原子面为(1011),(101),(011),(1101),(0111),(1011)将这十二个原子面分成两组,前三个和后三个原子面为一组,中间六个原子